[LeetCode] 1. Two Sum - Python

 

Disclaimer: 배워가면서 정리하고 있습니다. 개념에 오류가 있을 수 있습니다.

 

 

1. 문제

문제로 이동

배열에서 두 수를 더해 타겟 숫자를 만드는 인덱스를 찾는 고전 알고리즘 문제다.

• 주어지는 변수: 숫자 리스트 nums, 정수 target
• 반환해야 하는 값: nums 중에서 더해서 target이 되는 값의 각각의 인덱스 번호
• Assumption: 하나의 답만 있고 같은 인덱스를 두번 쓸 수 없다.

예시:

2. 답을 도출하는 방법

이 문제에서 답을 도출하는 방법은 여러가지가 있지만 크게 다음의 세 가지로 풀이된다.

1. 인덱스를 하나씩 더해보는 것 (brute force)

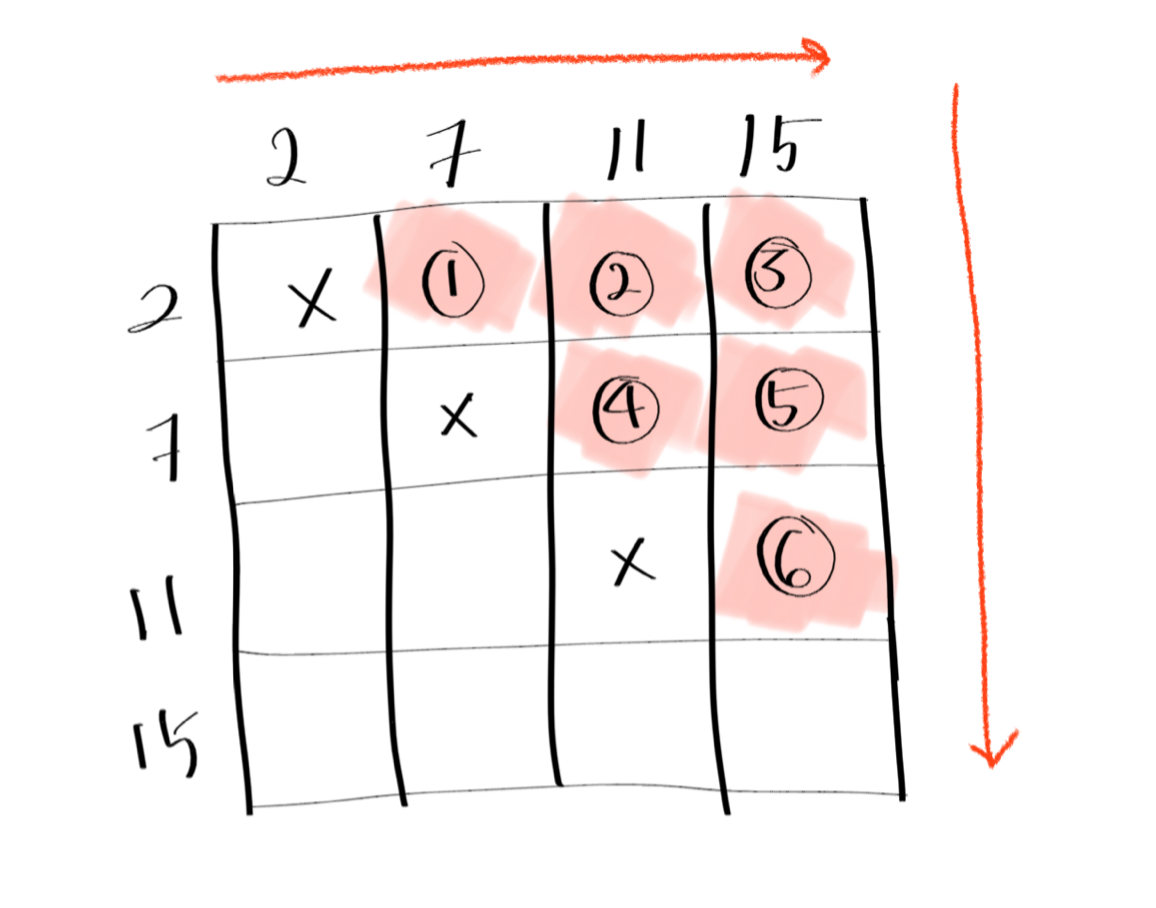
그림과 같은 방식으로 답을 도출하면 4*4 array를 계산 할 때 총 6번의 연산이 필요하다. 위의 brute force (하나씩 다 계산해 보는 것) 방식을 파이썬으로 나타내면 다음과 같다. 모든 쌍을 하나씩 다 더해보며 target이 되는 경우를 찾는 방식이다.

class Solution: 
    def twoSum(self, nums:List[int], target:int) -> List[int]: 
        for i in range(0, len(nums)): 
            for j in range(i + 1, len(nums)):
                if(num[i] + num[j] == target): 
                    return[i, j] 

• 장점: 코드가 쉽고, 누구든지 직관적으로 코드를 이해할 수 있다.
• 단점: 시간복잡도(O(n^2)가 높고 리스트에 수가 많아지면 급격히 느려진다.

데이터가 매우 적거나 단순 문제 이해 단계에서 추천하는 방법이다.

2. hashmap two-pass

먼저 배열을 한 번 순회하며 각 순자와 인덱스를 해시맵에 저장하고, 그 후 다시 배열을 돌며 "target-현재 숫자"가 해시맵에 존재하는지, 그리고 그게 자기 자신이 아닌지 체크해서 정답을 찾는 방식이다.

    def twoSum(self, nums:List[int], target:int) -> List[int]:
    hashmap = {}
    for i, num in emumerate(nums):
        hashmap[num] = i
    for i, num in enumerate(nums):
        diff = target - num 
        if diff in hashmap and hashmap[diff] != i:
            return[i, hashmap[diff]] 

• 장점: 처음 for 문에서는 단순 저장, 두번째 for 문에서는 lookup만 하므로 구현이 비교적 명확하다. 시간 복잡도와 공간복잡도 모두 O(n)으로 brute force 방식보다 단순하다.
• 단점: nums 리스트에 같은 숫자가 있을 때에는 hashmap에 마지막 인덱스만 남으므로 중복값 입력에서 주의가 필요하다.

3. hashmap one-pass

배열을 한번 훑으면서 현재값과 target-현재값이 해시맵에 있는지 체크하고, 있으면 해당 값을 반환, 없으면 현재 값을 해시맵에 저장하면서 진행하는 방식이다.

class Solution:
    def twoSum(self, nums:List[int], target:int) -> List[int]: 
     hashmap = {}
     for i, num in numberate(nums):
         diff = target - num
        if diff in hashmap 
            return [hashmap[diff], i]
         hashmap[num] = i 

• 장점: 효율성이 좋으면서 코드도 짧다. 시간이 O(n)이므로 가장 빠르다. 실전이나 인터뷰에서 가장 많이 사용된다. 중복값이나 다양한 인풋에 대부분 활용 가능하다.
• 단점: 다른 코드에 비해 초보가 이해하기 어렵다.

3. Terms:

시간 복잡도: 입력 데이터의 크기를 n이라고 했을 때, 알고리즘의 연산 횟수

• O(n): 알고리즘이 입력 데이터 크가에 정비례 해서 실행 시간이 늘어나는 경우. 예를들면 배열에 100개의 데이터가 있을 때 연산횟수는 100회.
• O(1): 입력 크기와 상관없이 실행 시간이 일정하다. 예를 들어 배열의 첫 번째 값을 가져오는 경우.
• O(n^2): 입력이 n이면 실행 횟수가 n^2.
• O(logn): 데이터가 많아질 때에도 실행 횟수가 느리게 증가함. 대표적으로는 이진탐색이 있음.
• 시간복잡도가 중요한 이유:

공간 복잡도: 알고리즘이 실행되는데 필요한 메모리 공간을 입력 크기에 대한 함수로 표현한 것

알고리즘 설계에서 시간과 공간은 종종 트레이드오프 관계이다. 시간을 절약하려면 더 많은 메모리를 사용해야 하고(해시테이블, 캐시 등), 공간을 절약하려면 더 많은 시간이 소모되는 경우가 대부분이다. 문제의 크기에 따라 적절한 알고리즘을 선택하는것이 필요하다.

4. 참고자료:

Gordon Zhu

 

NeetCode